Derivatives

One important concept in calculus is “Derivatives”. The concept is very important in Data Science & Machine Learning path. Let’s learn what are derivatives.
We take derivative at any point to show the change in the output \(\Delta y\) for a very small change in input \(\Delta x\).
This helps us understand, how a function would behave for small changes in the input values. To find derivative, we calculate the slope of the function at that point.
\(tan\theta\) which is perpendicular/base would also give us the derivative of function at that point.

Let’s find the derivative of a function \(x^{2}\) at a given point.

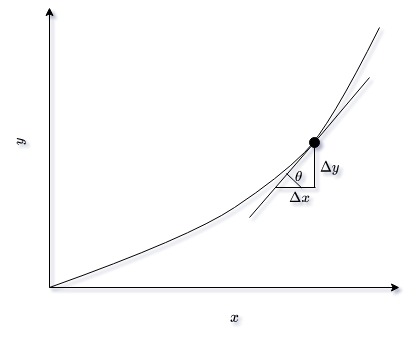
To find the derivative at any point, we calculate the slope at that point.

\[slope\ =\frac{small\ change\ in\ y}{small\ change\ in\ x} \ =\frac{\Delta y}{\Delta x}\]

Or we calculate the \(tan\theta\)

\[tan\theta \ =\frac{prependicular}{base} =\frac{\Delta y}{\Delta x}\]

Some important derivative rules that you should know about:

\[\frac{d\left( x^{n}\right)}{dx} =nx^{n-1}\] \[\frac{d( ln( x))}{dx} =\frac{1}{x}\] \[\frac{d( x)}{dx} =1\] \[\frac{d( c)}{dx} =0\ \ \ where\ c\ is\ any\ constant\] \[\frac{d( f( x) g( x))}{dx} =f'( x) g( x) \ +f( x) g'( x)\] \[\frac{d\left( f( x)^{n}\right)}{dx} =nf( x)^{n-1} f'( x)\] \[\frac{d( f( g( x)))}{dx} =f'( g( x)) .g'( x)\]

Knowing these rules we can now calculate the derivative of our function above \(x^{2}\).

\[\frac{d\left( x^{2}\right)}{dx} =2x^{2-1} =2x\]

So, the derivate of our function \(x^{2}\) would be \(2x\) at any point in our graph.